Nth Term Test
Introduction
If you study infinite series, you’ll meet the nth term test on day one.
It’s simple, powerful—and often misunderstood.
This guide explains what is the nth term test, how to apply nth term test for divergence, a practical nth term test calculator workflow, and common pitfalls to avoid.
You’ll get short rules, clear examples, and quick comparisons with the Ratio, Root, Integral, and Alternating Series Tests.
By the end, you’ll know exactly when the nth term test answers your question—and when you need another tool.
What is the nth term test?
Let ∑n=1∞an\sum_{n=1}^{\infty} a_n∑n=1∞an be a series with terms ana_nan.
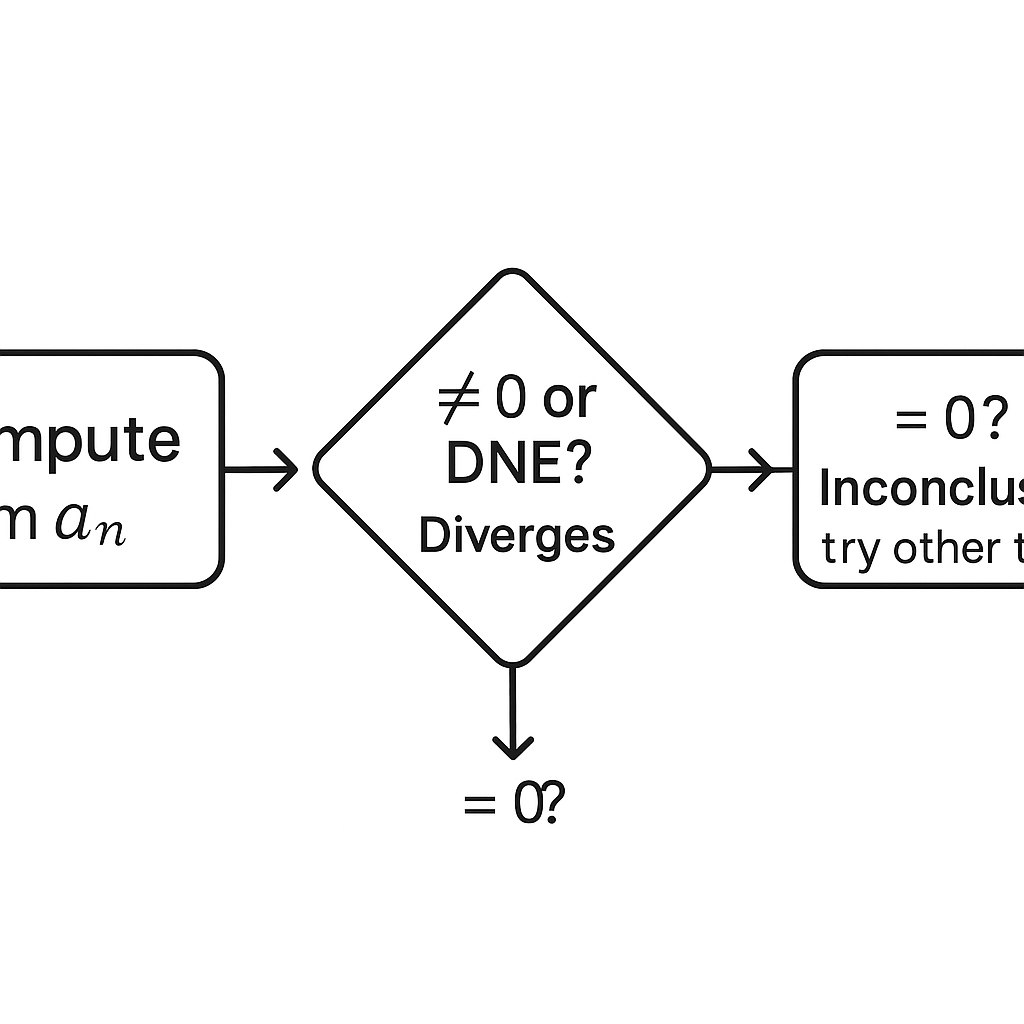
Nth Term Test (a.k.a. Test for Divergence):
If limn→∞an≠0\displaystyle \lim_{n\to\infty} a_n \neq 0n→∞liman=0 or the limit does not exist, then
∑n=1∞andiverges.\sum_{n=1}^{\infty} a_n \quad \text{diverges.}n=1∑∞andiverges.
Important: If limn→∞an=0\displaystyle \lim_{n\to\infty} a_n = 0n→∞liman=0, the test is inconclusive.
The series might converge or diverge—you must try another test.
Why it matters: For any convergent series, the terms must approach zero. If they don’t, partial sums can’t settle.
Nth term test for divergence (the use-case you’ll apply most)
The nth term test for divergence is a quick filter:
- Compute L=limn→∞an\displaystyle L = \lim_{n\to\infty} a_nL=n→∞liman.
- If L≠0L \neq 0L=0 or the limit doesn’t exist → series diverges.
- If L=0L = 0L=0 → no conclusion. Use another test.
Typical quick wins:
- If an→c≠0a_n \to c \neq 0an→c=0 (e.g., an=n+3n→1a_n = \frac{n+3}{n}\to 1an=nn+3→1) → diverges.
- If ana_nan oscillates without a limit (e.g., an=sinna_n = \sin nan=sinn) → diverges.
- If ana_nan decays too slowly—limit still 0, but beware (see examples).
Nth term test rules (and what they do not say)
Rules you can trust
- If liman≠0\lim a_n \ne 0liman=0 or DNE → series diverges.
- If liman=0\lim a_n = 0liman=0 → test is silent. You must try another test.
What the nth term test does not do
- It cannot prove convergence—ever.
- It cannot compare rates (e.g., exponential vs. polynomial) by itself.
- It does not handle alternating cancellation or monotonicity.
A practical “nth term test calculator” method (no fancy tool required)
Use this as your nth term test calculator workflow when you face a new series ∑an\sum a_n∑an.
Step 1 — Simplify ana_nan.
- Factor dominate terms.
- For rational functions, focus on highest degrees.
- For products, separate growth types (polynomial, exponential, factorial, log).
Step 2 — Take the limit L=limanL = \lim a_nL=liman.
- Rational functions P(n)Q(n)\frac{P(n)}{Q(n)}Q(n)P(n): compare degrees.
- degPPP < degQQQ → limit 0.
- degPPP = degQQQ → ratio of leading coefficients (nonzero).
- degPPP > degQQQ → ∞\infty∞ or −∞-\infty−∞.
- degPPP < degQQQ → limit 0.
- Exponentials vs. polynomials: cnc^ncn dominates nkn^knk.
- Factorials vs. exponentials: n!n!n! dominates cnc^ncn.
- Logs: logn\log nlogn grows slower than any nαn^\alphanα with α>0\alpha>0α>0.
Step 3 — Decide with the nth term test.
- If L≠0L \neq 0L=0 or DNE → diverges.
- If L=0L = 0L=0 → inconclusive → go to Step 4.
Step 4 — Choose the right follow-up test.
- Geometric form arna r^narn → Geometric Test.
- Factorials/exponentials → Ratio or Root Test.
- Positive terms with comparison → Comparison or Limit Comparison.
- Alternating → Alternating Series (Leibniz) Test.
- Integrable shape → Integral Test.
Worked examples (from easiest to tricky)
Example 1: an=n+3na_n = \dfrac{n+3}{n}an=nn+3
- liman=1≠0\lim a_n = 1 \neq 0liman=1=0.
- By the nth term test, ∑an\sum a_n∑an diverges.
- No further testing needed.
Example 2: an=1na_n = \dfrac{1}{n}an=n1 (harmonic series)
- liman=0\lim a_n = 0liman=0.
- Nth term test is inconclusive.
- Reality check: ∑1n\sum \frac{1}{n}∑n1 diverges (Integral Test or Cauchy Condensation).
Lesson: Limit 000 does not guarantee convergence.
Example 3: an=1n2a_n = \dfrac{1}{n^2}an=n21 (p-series with p=2>1p=2>1p=2>1)
- liman=0\lim a_n = 0liman=0.
- Inconclusive by nth term test.
- Using p-series knowledge (or Integral Test), ∑1n2\sum \frac{1}{n^2}∑n21 converges.
Example 4: an=(−1)nna_n = \dfrac{(-1)^n}{\sqrt{n}}an=n(−1)n
- liman=0\lim a_n = 0liman=0.
- Inconclusive by nth term test.
- Alternating Series Test: terms decrease to 0 and alternate sign → series converges conditionally.
Example 5: an=1lnna_n = \dfrac{1}{\ln n}an=lnn1 for n≥3n \ge 3n≥3
- liman=0\lim a_n = 0liman=0.
- Inconclusive by nth term test.
- Cauchy Condensation / comparison shows ∑1lnn\sum \dfrac{1}{\ln n}∑lnn1 diverges.
Lesson: Very slow decay can still diverge.
Example 6: an=0.9na_n = 0.9^nan=0.9n
- liman=0\lim a_n = 0liman=0.
- Inconclusive by nth term test.
- Geometric Test with ∣r∣=0.9<1|r|=0.9<1∣r∣=0.9<1 → ∑0.9n\sum 0.9^n∑0.9n converges.
Example 7: an=sinna_n = \sin nan=sinn
- sinn\sin nsinn does not have a limit as n→∞n\to\inftyn→∞.
- By the nth term test, ∑sinn\sum \sin n∑sinn diverges.
Example 8: an=n!2na_n = \dfrac{n!}{2^n}an=2nn!
- Terms grow without bound → liman=∞\lim a_n = \inftyliman=∞.
- Nth term test → diverges.
- (Ratio Test also flags divergence.)
How the nth term test compares to other tests
Use this quick guide to pick the next tool when the nth term test is inconclusive.
- Ratio Test — best for factorials and exponentials (e.g., n!n!n!, cnc^ncn, power series).
Try next: Ratio Test - Root Test — great for expressions with nnnth powers/roots or absolute values.
Try next: Root Test - Integral Test — when an=f(n)a_n=f(n)an=f(n) with fff positive, continuous, decreasing.
Try next: Integral Test - Alternating Series Test (Leibniz) — for (−1)nbn(-1)^n b_n(−1)nbn with bn↓0b_n\downarrow 0bn↓0.
Try next: Alternating Series Test - Comparison / Limit Comparison — for positive-term series you can bound above/below.
Try next: Comparison Test
Rule of thumb:
Start with the nth term test. If it doesn’t settle the case, choose the test that matches your term’s structure.
Common mistakes and how to avoid them
- Mistake 1: “Limit 0 means converge.”
Wrong. It only removes one obvious reason to diverge. - Mistake 2: Testing partial sums instead of terms.
The test uses ana_nan, not the partial sums SnS_nSn. - Mistake 3: Ignoring oscillation.
If ana_nan doesn’t have a limit, that’s enough to declare divergence. - Mistake 4: Forgetting absolute vs. conditional convergence.
A series can converge conditionally even if ∑∣an∣\sum |a_n|∑∣an∣ diverges. - Mistake 5: Overusing L’Hôpital’s Rule.
Often you only need degree comparison or dominance ideas.
Quick answers (FAQ)
What is the nth term test?
A divergence test: if liman≠0\lim a_n \ne 0liman=0 or DNE, the series diverges. If the limit is 0, it’s inconclusive.
Is the nth term test the same as “test for divergence”?
Yes—two names for the same criterion.
What does the nth term test for divergence prove?
Only divergence. It never proves convergence.
What are the nth term test rules?
Compute liman\lim a_nliman. Non-zero or nonexistent limit → diverge. Zero limit → no conclusion.
Is there an nth term test calculator?
You don’t need one. Follow the workflow above: simplify ana_nan, take the limit, decide, and if needed, choose the next test.
When should I not use the nth term test?
Never as a sole tool to “prove convergence.” Use it as a first filter, then switch tests based on the term’s structure.
Conclusion
The nth term test is your quickest divergence check: if the term’s limit isn’t zero—or doesn’t exist—the series must diverge. It catches obvious cases like constant tails, oscillations, or terms that grow. Think of it as a gatekeeper: fail the limit-to-zero requirement and you’re done—no deeper test needed.
If the limit is zero, the story isn’t over; the test simply can’t decide. Famous counterexample: the harmonic series has terms going to zero yet still diverges. That’s why you pivot to the right follow-up test based on structure—geometric patterns, factorials/exponentials, alternating signs, or integrable shapes.
When you switch tools, match the anatomy of ana_nan: Ratio/Root for factorials and powers, Alternating for sign flips, Comparison/Limit Comparison for positive terms, Integral for smooth, decreasing functions. Drop your trickiest example in the comments—tell me the term ana_nan and what you tried—and I’ll walk you through the next best test step by step.
Stay in touch to get more updates & alerts on Sosomodapks! Thank you